Frino, Alex; Wearin, Grant; Fabre, Joel --- "Do Returns on Synthetic Portfolios Constructed from Stock Index Futures Deliver Capital Gains, Dividends and Franking Credits? " [2004] JlLawFinMgmt 2; (2004) 3(1) Journal of Law and Financial Managment 8

• Do Returns On Synthetic Portfolios Constructed From Stock Index Futures Deliver Capital Gains, Dividends And Franking Credits?
• Abstract
• 1. Introduction
• 2. Do Stock Index Futures Deliver Dividends And Franking Credits?
• 3. Data And Method
• 4. Empirical Analysis
• 5. Summary And Conclusion
• Endnotes

---

Do Returns on Synthetic Portfolios Constructed from Stock Index Futures Deliver Capital Gains, Dividends and Franking Credits?

By Alex Frino, Grant Wearin & Joel Fabre*

Abstract

Previous papers documenting the relationship between returns on stock index futures and stock indices typically ignore dividends¹. This appears to leave open the issue of whether the return on a synthetic position constructed using stock index futures and a risk free asset efficiently delivers the value of dividends. This paper proves mathematically that the returns on synthetic positions using such contracts should deliver capital gains, cash dividends and the value of franking credits derived by arbitrageurs. Empirical evidence consistent with this proposition is provided, using a sample of data for the SPI 200 contract trading on the Sydney Futures Exchange. Interestingly, the evidence suggests that franking credits are priced into stock index futures contracts, despite the introduction of the 45-day rule which seemingly would appear to prevent this.

JEL Classification: G11; G12; G13; G28

Keywords: Synthetic portfolios, stock index futures, dividends, franking credits

1. Introduction

With the proliferation of managed funds in the last three decades, stock indices continue to play a central role in benchmarking the performance of equity fund managers. This is especially the case for index managers, who face the fundamental challenge of minimizing tracking error - the absolute difference between the fund return and the index return - while controlling transaction costs². This has contributed to the development of financial instruments such as stock index futures, which enable investors to obtain index exposure synthetically, that is, without physically trading stocks³. Compared to alternatives such as exchange-traded-funds or index options, index futures offer the lowest cost method of investing in stock indices⁴. However, a common misconception is that use of these contracts necessitates the sacrifice of stock dividends⁵. We provide a mathematical proof supporting the notion that a synthetic position made up of stock index futures contracts and a risk free asset can synthetically generate the return obtained by investing in each stock in the index portfolio. Prior academic literature documenting the relationship between returns on stock index futures and stock indices, focusing on hedging effectiveness, typically ignores dividends⁶. All of these studies examine price indices, which omit dividends. This appears to leave open the issue of whether the return on a synthetic position constructed using stock index futures and a risk free asset effectively delivers the value of dividends. This is doubly important in jurisdictions such as Australia where franking credits are attached to dividends, and raises the question of whether synthetic positions also deliver franking credits. These issues are particularly relevant to fund managers, who are typically benchmarked to accumulation indices, which include dividends.

This paper provides new evidence on the relationship between returns on stock index futures and stock indices by examining whether the returns to synthetic positions constructed using stock index futures and a fixed income security deliver capital gains, dividends and franking credits. It is proven mathematically that if franking credits are priced into a stock index futures contract by arbitrageurs, then returns on synthetic positions constructed using a fixed income security and stock index futures deliver capital gains, cash dividends and the value of franking credits derived by arbitrageurs. Empirical evidence consistent with this proposition is also provided, using a sample of data for the SPI 200 contract trading on the Sydney Futures Exchange (SFE). The analysis demonstrates that a synthetic position constructed using the SPI 200 and a Bank Accepted Bill (BAB) outperforms the return on the S&P/ASX 200 Accumulation Index. Furthermore there is a significant positive relationship between outperformance and franking credits paid out by the index. Interestingly, one of the implications of this empirical evidence is that franking credits are priced into stock index futures contracts, despite the introduction of the 45-day rule which seemingly would appear to prevent this.

The remainder of this paper is organized as follows. Section 2 proves mathematically that the returns to synthetic positions using stock index futures and a fixed income security deliver capital gains, dividends and franking credits. Section 3 describes the data used in the empirical analysis. Section 4 provides empirical analysis of the performance and effectiveness of the synthetic position in delivering the value of dividends and franking credits. Section 5 concludes.

2. Do Stock Index Futures Deliver Dividends And Franking Credits?

A fundamental choice for index managers is whether to replicate index returns directly by purchasing the underlying stocks, or synthetically through the use of instruments such as index futures. To replicate the return on an index, an investor needs to generate the return that would be achieved by holding the stocks in the index portfolio, with the correct weightings. Before taxes and transaction costs, this return comprises capital gains, dividends and any franking credits attached to the dividends. Therefore, delivery of the value of dividends and any attached franking credits contributes to the efficacy of a replication strategy. Because index futures are normally based on price indices, there may be a perception that returns obtained from replication strategies using index futures do not deliver the value of dividends or franking credits. However, when combining index futures with a risk free asset to create a synthetic position the returns will accrue dividends. The proof below demonstrates that the returns to a synthetic position comprising a long position in an index futures contract and a fixed income security, in fact, replicate the return to an accumulation index.

There are several assumptions underlying the proof. First, the proof relies on the linear cost-of-carry model to value the futures contract, which implies an assumption that the futures trade at fair value. Second, it is assumed that the interest rate representing the financing cost in the cost-of-carry model is approximately equal to the rate of return on the bond. To the extent that either of these assumptions do not hold, there will be some tracking error between the returns of the index portfolio and the synthetic position. Third, for each exposition we ignore the re-investment of dividend returns that accrue to the synthetic position⁷.

Index Portfolio Return

From one point in time T-1 to another T, the return on all stocks comprising the index portfolio when dividends are re-invested is precisely the same as the return on an accumulation index. In notational format:

where: (1)

I_T is the value of the index portfolio at time T

d_t is the dividend paid out by the index portfolio over period t (i.e., from T-1 to T).

Synthetic Position Return

The return on a synthetic position is given by the return on the futures contract plus the return on the bond from T-1 to T. Since the investment in the futures contract is costless, then the cost of the portfolio is simply the value of the index portfolio (I_T-1) which represents the amount of cash available for investment in the bond. Denoting the price of the futures contract at time T as f_T, then the return on the synthetic position r’_p is given by the following expression:

where: 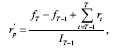(2)

is the return on the bond in dollars from T-1 to T.

Index Portfolio and Synthetic Position Equivalence

To prove that the return on the synthetic position given by (2) is equivalent to the return on the index portfolio including dividends (1) we begin by stating the cost-of-carry model which implies that the futures price f_T can be written as follows:

where: (3)

d_t is the dividend paid (in dollars) by the index portfolio in period t

rt is the opportunity or financing cost of investing in the index portfolio

n is the maturity date of the futures contract.

Using (3) the futures price f_T-1 can be written as follows:

. (4)

Substituting (3) and (4) into (2) yields:

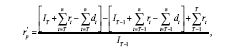
which can be re-arranged and simplified as follows:

Since (5) is identical to (1), we have proven that the return on the synthetic position is equal to the return on the index portfolio plus dividends. If dt is defined as the value of dividends including franking credits, then trivially from (5), it follows that the synthetic position will return the value of franking credits as well as dividends.

3. Data And Method

The empirical analysis focuses on a widely used Australian benchmark index, the S&P/ASX 200. Data on the cash index, associated dividends and franking credits, SPI 200 index futures and returns on BABs were gathered for the period September 1, 2001 to September 30, 2003⁸. Closing prices for the accumulation and price indices were downloaded from the S&P website. The index file contains closing index values, which are calculated and disseminated by S&P at 4:05 p.m. on each trading day. S&P calculates closing index values using the closing prices of constituent stocks, determined in the SEATS call auction for each stock at approximately 4:05 p.m.

Transaction data for SPI 200 futures were provided by the SFE. The SFE file describes the prices of trades for the contract nearest to expiry and the next nearest contract, and is time-stamped to the nearest second. The last price transacted before 4:05 p.m. were extracted from the SFE files. Only prices recorded at 4:05 p.m. were used as these are synchronized with ASX closing prices upon which the underlying index is calculated. The 25-minute difference in closing times would result in error in the measurement of tracking error if reported futures closing prices were used⁹. Data on 90-day BABs were gathered from a file containing a daily time-series of BAB yields, provided by the Reserve Bank of Australia.

A daily time-series of accumulation and price index returns, SPI 200 returns and 90-day BAB yields was constructed by joining the files described above. The limited life of futures contracts requires ‘rolling over’ to the next contract as the near contract expires in order to create a long-term series of futures returns. Prior research has shown that rolling over at the expiry date induces spurious volatility and autocorrelation in futures returns¹⁰. As a robustness check against ‘expiry effects’, separate futures return series were constructed from price series rolled over at 1, 5, 10, 15 and 20 days before expiry. A month-end file containing the accumulation and price index (log) returns, five futures series (log) returns and one BAB yield was then constructed by summing daily data within each calendar month¹¹. The final sample consists of a time-series of 25 months of data.

The return on the synthetic position is calculated by assuming the value of the index portfolio is invested in the fixed income security. This represents the same amount of funds that would be allocated among component stocks of the index portfolio had the investment taken place in the physical market. At this point one long SPI200 futures contract is bought. The investment in the fixed income security and the stock index futures contract combine to create the synthetic position. Mathematically the return on the synthetic portfolio is:

Where: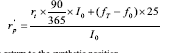

r’_p is the return to the synthetic position

r_t is the annual return on the risk free fixed income security

I₀ is the price index at time 0 in dollars

(f_T - f₀) x 25 is the dollar gain / loss on the futures component of the synthetic position assuming the futures position is rolled at time T, approximately 90 days from time 0.

4. Empirical Analysis

Relative performance of synthetic position

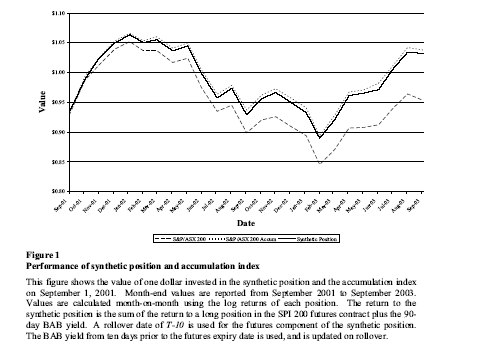
Figure 1 illustrates the value of one dollar invested in the synthetic position and the accumulation index on September 1, 2001. The return to the synthetic position is the sum of the return to a long position in the SPI 200 futures contract plus the 90-day BAB yield. Over the sample period, the synthetic position outperforms the price index strongly (which ignores dividends), and tracks the accumulation index closely, although there is evidence that it slightly underperforms. Prima facie, it appears that the synthetic portfolio returns the bulk of the dividend yield paid out by the index portfolio. A rollover date of T-10 for the futures is used¹². It is possible that transaction costs associated with rollover of the futures component of the synthetic position in expiration months are adversely affecting the performance of the synthetic position¹³. Hence the sample is partitioned into expiration months (i.e., March, June, September and December) and non-expiration months.

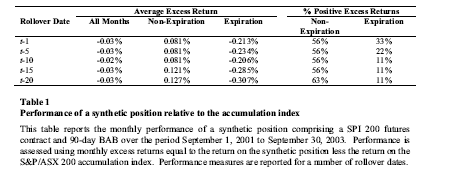
Excess returns equal to the difference between the synthetic position return and the accumulation index return are calculated to analyse the relative performance of the synthetic position. A positive excess return indicates that the synthetic position has outperformed the accumulation index, while negative excess returns indicate underperformance. Table 1 reports the average excess returns over the sample period for expiration and non-expiration months, separately and combined. Also reported are the proportion of months with a positive excess return, broken down by expiration and non-expiration months. Separate results are reported for each rollover date. (see Figure 1)

The results reported in Table 1 reveal substantial differences in performance between the synthetic position and the accumulation index. When all months are combined, the synthetic position slightly underperforms the accumulation index. Average excess returns in expiration months range from underperformance of 20.6 basis points to 30.7 basis points, depending on the rollover date used. Substantial underperformance in expiration months is likely due to the transaction costs incurred in rolling over the futures component of the synthetic position around expiry. However in non-expiration months, average excess returns vary from +8.1 basis points to +12.7 basis points - hence the synthetic position generally outperforms. The proportion of months with positive excess returns in non-expiration months also greatly exceeds that in expiration months. These results suggest that the synthetic position outperforms the accumulation index in non-expiration months, in fact, in almost two-thirds of the months examined. This could be due to the ability of the synthetic position to deliver the value of franking credits to investors (which are not included in returns based on the S&P/ASX200 Accumulation Index). A repeat test of the relationship between the synthetic return and the franking credit yield of the index follows.

Additional tests

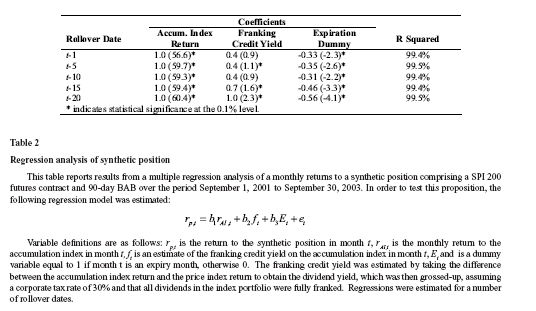
If arbitrageurs are able to extract dividends as well as a proportion of franking credits from the index portfolio when holding an arbitrage position, the capital gain on the futures and hence the outperformance of the synthetic position relative to the accumulation index should be higher in months where franking credits are higher. In order to test this proposition, while controlling for transaction costs associated with rollover in expiration months, the following regression model was estimated:

Where:

r_p,t is the return to the synthetic position in month t

r_AI,t is the monthly return to the accumulation index in month t

f_t is an estimate of the franking credit yield on the accumulation index in month t

E_t is a dummy variable equal to one if month t is an expiry month, otherwise zero.

The franking credit yield was estimated by taking the difference between the accumulation index return and the price index return to obtain the dividend yield, which was then grossed-up, assuming a corporate tax rate of 30 percent and that all dividends in the index portfolio were fully franked.

Estimates of the model above can be used to assess whether the return on the synthetic position delivers the value of dividends and capital gains, in which case the coefficient should be close to one. Also, whether the return on the synthetic position is related to the franking credit yield of the index can be assessed by examining b₂, which should be positive and significant if arbitrageurs can extract the value of franking credits from the index portfolio. Any underperformance during expiration months is captured in the coefficient b₃.

Table 2 sets out the results of the analysis. As expected, the coefficient b₁ is approximately equal to 1 and highly significant for all rollover dates, consistent with the proposition that the synthetic position delivers the value of dividends in addition to capital gains.

Two other very important results are reported in Table 2. First, there is evidence that the relationship between the performance of the synthetic position and the franking credit yield is positive and significant. The result implies that the synthetic position also delivers outperformance which is related to the value of franking credits paid out by the index, after controlling for expiration effects. Second, and importantly, the coefficients on the expiration dummy variable suggest that the synthetic position appears to significantly underperform by between 31 and 56 basis points in expiration months (depending on the rollover date).

Interestingly, one of the implications of the results is that franking credits are priced into stock index futures contracts despite the introduction of the 45-day rule in July 1997, which seemingly appear to prevent this. Under the 45-day rule, investors not holding stock continuously for 45 days around dividend payment periods are not entitled to franking credits¹⁴. If the 45-day rule is adhered to there should be no positive relationship between the return on the synthetic position and the franking credit yield. Arbitrageurs would not be entitled to franking credits on stocks held for less than 45 days and subsequently could not price them into the futures contract. However, there is anecdotal evidence suggesting that arbitrageurs are able to avoid the 45-day rule and extract the value of franking credits through carefully constructed transactions¹⁵. In the presence of such transactions there exists plausible justification for the pricing of franking credits into futures contracts and a positive and significant relationship between a synthetic portfolio and franking credit yield. The empirical evidence provided by this paper is therefore consistent with anecdotal evidence of avoidance of the 45-day rule.

5. Summary And Conclusion

This paper proves mathematically that returns on synthetic positions using stock index futures contracts and a fixed income security should deliver capital gains as well as the value of dividends derived by arbitrageurs. Consistent with this proposition, the empirical evidence provided in this paper reveals that a synthetic position comprising a long position in a stock index futures contract plus a bond, delivers the value of capital gains and dividends, plus a proportion of the value of franking credits. This is despite the provisions of the Income Tax Assessment Act (specifically, the 45-day rule), which intend to prevent arbitrageurs from obtaining the value of franking credits and consequently pricing them into the futures contract. The results also highlight that the adverse performance of the synthetic position in expiration months potentially negates any outperformance achieved in non-expiration months. The rollover strategy used is therefore a key factor in unlocking the full benefit of synthetic positions involving index futures. The findings in this paper also suggest that previous research which assesses the tracking efficiency of stock index futures contracts against price indices need to be revisited - returns from synthetic exposure need to be assessed against accumulation indices.

Endnotes

* Alex Frino is ccorresponding author and a Professor of Finance at the University of Sydney. Postal: Finance Discipline, Building H69, University of Sydney, NSW, Australia, 2006. Telephone: [phone]. Fax: [phone]. E-mail: [e-mail]. Grant Wearin is a doctoral candidate at the School of Business, University of Sydney and Joel Fabre is an associate lecturer at the School of Business, University of Sydney.

[1] Phil Holmes, “Stock Index Futures Hedging: Hedge Ratio Estimation, Duration Effects, Expiration Effects and Hedge Ratio Stability” (1996) 23 Journal of Business Accounting and Finance 63-77.

[2] Martin Gruber, “Another Puzzle: The Growth in Actively Managed Mutual Funds” (1996) 55 Journal of Finance 783-810; Alex Frino and David Gallagher, “Tracking S&P 500 Index Funds” (2001) 28 Journal of Portfolio Management 44-55; Alex Frino and David Gallagher, “Is Index Performance Achievable?: An Analysis of Australian Equity Index Funds” (2002) 28 Journal of Portfolio Management 44-55.

[3] The first stock index futures contract, covering the Value Line Index, was listed by the Kansas City Board of Trade in February, 1982. All Ordinaries index futures were listed by the SFE in February, 1983. On May 2, 2000, the SFE listed SPI 200 futures to reflect the change to the S&P/ASX 200 as the broad-based benchmark.

4. John Fleming, Barbara Ostdiek and Robert Whaley, “Trading Costs and the Relative Rates of Price Discovery in Stock, Futures and Option markets” (1996) 16 Journal of Futures Markets 353-387; Lorne Switzer, Paula Varson and Samia Zghidi, “Standard and Poor’s Depositary Receipts and the Performance of the S&P 500 Index Futures Market” (2000) 20 Journal of Futures Markets 705-716.

[5] An earlier version of this paper was workshopped amongst fund managers. We were surprised by the large number of managers that initially held the view that because the SPI 200 futures contract is settled against a price index, a synthetic position would not deliver dividends (let alone franking credits).

[6] Stephen Figlewski, “Hedging Performance and Basis Risk in Stock Index Futures” (1984) 39 Journal of Finance 657-669; Phil Holmes, “Stock Index Futures Hedging: Hedge Ratio Estimation, Duration Effects, Expiration Effects and Hedge Ratio Stability” (1996) 23 Journal of Business Accounting and Finance 63-77; Juan Lafuente and Alfonso Novales, “Optimal Hedging Under Departures from the Cost-of-Carry Valuation: Evidence from the Spanish Stock Index Futures Market” (2003) 27 Journal of Banking and Finance 1053-1078.

[7] Allan L. Tucker, “Financial Futures, Options and Swaps”, 1991, pp. xx - yy.

[8] The S&P/ASX 200 was first introduced on March 31, 2000. We begin our analysis from September 1, 2001 to avoid the unusual expiration effects in June 2001, where an alleged manipulation of the SPI 200 occurred on settlement (Jemima Whyte, “ASX Fines Broker for Breaking Rules” (December 17, 2002) Australian Financial Review).

[9] Analysis using reported futures closing prices revealed that tracking error would be overstated by a margin of up to 17 basis points.

[10] Christopher Ma, Jeffrey Mercer and Matthew Walker, “Rolling Over Futures Contracts: A Note” (1992) 12 Journal of Futures Markets 203-217.

[11] The return on the fixed income component of the synthetic position is adjusted for each rollover date. For example, a rollover occurring on day T-20 uses the BAB yield from twenty days prior to the futures expiry date. The BAB yield is updated on rollover.

[12] Analysis using rollover dates of 1, 5, 15 and 20 days prior to expiry produced similar results.

[13] Alex Frino and Michael D. McKenzie, “The Pricing of Stock Index Futures Spreads at Contract Expiration” (2002) 22 Journal of Futures Markets 451 - 469.

[14] Days where a risk-reducing transaction or arrangement are in place (i.e., transactions related to hedging) are not counted as part of the 45 days. Under the 45-day rule, a maximum delta of 0.7 for delta style hedges is allowed.

[15] Stuart Washington, “Not Guilty Says Macquarie” (2003) 25 Business Review Weekly 22.