
eJournal of Tax Research


|
Home
| Databases
| WorldLII
| Search
| Feedback
eJournal of Tax Research |

|
Fabrizio Bulckaen and Marco Stampini[♣]
This paper deals with efficiency and distributional effects of marginal commodity tax reforms in economies with heterogeneous individuals. It contributes to the literature in three ways. First, a decision rule based on revenue potentialities – the ratio between marginal revenue and the tax base - is originally developed with reference to a many consumers economy. The relevance lies in the fact that these indicators do not depend on measures of utility. Second, the connection with former literature is analyzed. Third, a comprehensive and progressive decision-making procedure relying on revenue potentialities is defined. Overall, all that policy makers need to know – in order to look for improvements in efficiency and/or distribution through revenue-neutral marginal commodity tax reforms – is the revenue potentiality of each tax and the share of expenditure by poor families. An example with reference to Italian data is provided.
This article deals with efficiency and distributional effects of revenue-neutral marginal commodity tax reforms[1]. The paper contributes to the literature in three ways. First, it originally develops a rule based on revenue potentialities – defined as the ratio between marginal revenue and the base of a tax – for decisions in a context characterized by many and heterogeneous consumers. Revenue potentialities have important relevance for policy making because they do not depend on measures of utility. Second, the connection with former literature is analyzed, in order to make as clear as possible the relationship between efficiency and distribution of welfare. In particular, we consider the work of Ahmad and Stern (1984) – based on the specification of social weights in the social welfare function – and of Yitzhaki et al. (Yitzhaki and Thirsk (1990); Mayshar and Yitzhaki (1991)) – looking for welfare dominating reforms. Third, we define a procedure that policy makers interested both in efficiency and distribution can follow when searching for welfare improving opportunities, consistently with the indications of the theory. An explanatory application is provided with reference to Italian data.
The literature on tax reforms differs from the one on optimal taxation because it deals with marginal changes starting from any sub-optimal initial situation. Instead of looking for the optimal tax rate structure, it searches for directions of potential improvement, for small changes that increase welfare. The main advantage of this approach is that it requires a much smaller amount of information. It is not necessary to know the whole shape of consumers demand functions, but only their reaction to price changes, moving from the observed starting point[2].
Recent developments in the literature on tax reforms – building on the work of Atkinson and Stiglitz (1976) – suggest that differential commodity taxation is not justified. This implies that there is no reason for studying commodity tax reforms, as a welfare improvement can be obtained by reducing commodity tax differentials, even starting from a non-optimal situation in terms of (non-linear) income tax (Kaplow, 2004). At the limit, it would be advisable to remove commodity taxes altogether. Nonetheless, we think that valid reasons exist for studying commodity tax reforms. First, the conclusions of Kaplow (as the author repeatedly states), as well as those of Atkinson and Stiglitz, fundamentally depend on the assumption of weak separability between leisure and other goods in the consumers’ utility function – an assumption that we do not make. If labor supply does not depend on commodity prices, it is obvious that differentials in commodity taxes introduce a distortion in the choice among commodities, without any positive effect on the distortion in the choice between leisure and other goods. However, without this crucial assumption of separability, the commodity tax structure needs not being uniform and commodity taxation has theoretical justification. In addition, commodity taxation could be justified also for other reasons. When information is imperfect, it may be that commodity taxes are less vulnerable to evasion than income taxes. Commodity taxes can also be Pigovian and designed to correct externalities. We do not deal with these and other justifications in the present paper (though our model could accommodate externalities), but feel confident in saying that governments may well be interested in finding ways to reform the existing commodity tax system (without removing it), with positive effects on efficiency and distribution.
Within the literature on commodity tax reforms, two main lines of research can be distinguished: one dealing with efficiency only, in a single consumer economy; the other taking into account also distributional considerations.
Within the former stream, starting from Corlett and Hague (1953-54), the literature has suggested that policy makers should consider each tax marginal distortion, i.e. the welfare cost of raising an extra unit of general revenue by increasing a single tax rate. If the marginal cost of funds raised through different taxes differ, then welfare can be increased by reducing the rate of most distortionary taxes and increasing the rate of less distortionary ones, in order to keep revenue constant. Hatta (1986) provides a more intuitive and easy to implement rule based on tax rates only. He shows that the optimal tax rate structure is close to uniform, so that (under certain conditions regarding substitutability) welfare can be increased by reducing high rates and increasing low ones. Bulckaen and Stampini (2001) study the efficiency effects of commodity tax reforms in presence of environmental externalities through the comparison of revenue potentialities, defined as the ratio between the marginal revenue of a tax and its base. The authors stress the independence of the indicator from measures of utility. These rules, however, are concerned with efficiency only and do not give any relevance to distributional considerations, i.e. to the aversion towards inequality which characterizes social preferences.
When different consumers are considered, Ahmad and Stern (1984) show that tax reforms can still be analyzed on the base of the marginal cost of public funds raised through different taxes. These, however, are now a function of both the effect on efficiency and of the distributional characteristics[3] of the affected goods. In order to identify welfare improving tax reforms, the policy maker must make social weights explicit [4].
Ahmad and Stern obtain their results under the strong assumption of fixed labor supply. The general framework of the analysis and the main formulas are not affected (suggesting that the authors could have waited to introduce the restriction later on in the paper, when discussing particular cases), but interpretations and implications are. In fact, Ahmad and Stern find that only distributional considerations can motivate a departure from uniform commodity taxation. This is due to the fact that, with fixed labor supply, uniform commodity taxation corresponds to a proportional tax on fixed total wage, hence to a lump-sum tax. The assumption is removed by Gordon (1989), who develops his model in terms of compensated demand functions. Unfortunately, Gordon obtains far less intuitive expressions for the marginal distortions caused by different taxes, which allow for intuitive results only under very specific assumptions – preferences identical among consumers, separable between goods and labor and quasi-homothetic in goods[5].
An important progress is made by Yitzhaki and Thirsk (1990), who study the possibility – starting from any sub-optimal tax rate structure – to identify revenue neutral tax reforms desirable under (almost) any social welfare function. More specifically, they look for revenue-neutral tax reforms desirable according to any social welfare function characterized by a non-negative degree of aversion to inequality. The only necessary condition is that poor people’s welfare is weighted at least as much as rich people’s, but these weights do not need to be declared explicitly. The analysis can be carried out through two sets of information. First, it is necessary to know the marginal distortion of each tax – i.e. the marginal welfare loss caused by raising one additional unit of revenue through each tax. Second, it is necessary to know how consumption is distributed among different households – i.e. to know the concentration curves[6]
. The convenience of tax reforms can be enquired by comparing concentration curves multiplied by the respective marginal cost of funds. If one of them lies below another along the whole population range (stochastic dominance), then there is no need to define social weights: a social welfare improving tax reform is possible.
In a related paper, before focusing on stochastic dominance, Mayshar and Yitzhaki (1995) show that the marginal social cost of raising funds (a measure of the marginal distortion) can be decomposed into the product of the distributional characteristic of the good and the marginal efficiency cost of funds. While this suggestion has remarkable empirical relevance, and related indications can be found in the previous (Ahmad and Stern (1984)) and later literature (Slemrod and Yitzhaki (1996), Yitzhaki (2003)), theoretical and applied works on the evaluation of tax reform have failed giving it the deserved importance.
The present paper originally develops the use of revenue potentialities for the evaluation of commodity tax reforms in economies with heterogeneous individuals, where both efficiency and distribution of welfare matter. A simple model with two groups of families – the rich and the poor, represented by two individuals – is employed. The development of the model allows defining a procedure that the policy maker can follow in order to identify welfare increasing opportunities, starting from the lowest amount of hypothesis, structure and information. When the most desirable opportunities are not available, the policy maker can identify welfare improving tax reforms only by imposing more structure. Operationally, the first step is to study the effects of the reform in terms of efficiency, by measuring the revenue potentiality of different taxes. These indicators can be used together with information on the distribution of consumption[7] in order to identify reforms which increase welfare according to any social welfare function characterized by a non-negative degree of aversion towards inequality. If such reforms are not possible, the policy maker is required to express some social weights. This allows identifying the overall welfare effect of the reform the policy maker is interested in, as well as distinguishing between effects on efficiency and on distribution of welfare. The policy maker interested in a particular tax reform can also calculate the minimum degree of preference for the worse-off group (with respect to the better-off) necessary to make the reform socially desirable.
This procedure is applied to the Italian tax system in order to provide an example of how welfare improving opportunities through tax reforms can be looked for. We show that the information set necessary for a quite intuitive analysis is not too big and difficult to collect – being limited to marginal revenues of the taxes and distribution of consumption.
The paper is organized as follows. The next Section develops the theoretical model and defines a viable decision making procedure. The following Section provides an example of empirical analysis, identifying reforms which improve efficiency and/or distribution. The last Section concludes, with some policy recommendations.
We consider a two individuals economy. In general, these individuals can be seen as two groups of families, the rich and the poor. The generalization to H individuals (H>2) is straightforward (and is reported in Appendix); at this stage we keep things as simple as possible.
Two individuals (j = A, B) derive utility from leisure (![]()
,![]()
), from the consumption of n commodities (![]()
,![]()
; i=1,...n) and from a public good provided by the State (r). As usual in the literature, we assume that the public good is weakly separable from commodities and leisure in the utility functions, hence demands for commodities and leisure do not depend on r. The uncompensated demand functions are represented for each consumer by the vector x (with dimension n+1), which depends on the vector of consumption prices q and on the exogenous income y [8]:
![]()
(1).
Exogenous incomes are assumed to be equal to zero. The two individuals differ
in the utility function, which determines a different
allocation of time between
labor and leisure, hence a different earned income. Net demand for leisure is
negative (![]()
,![]()
), so that labor supply is positive for both individuals. The individual budget constraints are given by:
![]()
(2).
Production is described by a linear technology, with labor by the two individuals as the only factor of production:
![]()
(3),
in which p is a vector of positive constants.
We exclude the presence of lump sum taxes; hence, the public sector draws tax revenue through proportional taxes only.
Because of our assumption of constant returns to scale, we can normalize production and consumption prices assuming leisure as the untaxed good[9]. Furthermore, in order to simplify the analysis, we define the units of measure in order to obtain all constants of the production function and all production prices equal to one (p = ι, vector of elements equal to 1). Hence, consumption prices are given by the following expression:
![]()
(4),
where ti is the i-th element of t, vector of tax rates, and t0=0.
Total tax revenue is used to purchase the public good r. In order to analyze the welfare effect of a reform which (for example) increases the tax rate on good 1 and recycles the additional revenue by reducing the rate on the arbitrary good n, we differentiate the social welfare function:
![]()
(5),
where V is the indirect utility function. Using Roy’s identity, we obtain:
![]()
(6),
where ![]()
represents the social evaluation of the marginal utility of individual j ’s income (j=A, B), which corresponds to the weight in the social utility function (we will later assume that the policy maker does not assign higher priority to individual B’s utility, so that γA≥γB). By definition of the reform, dt1>0 and dtn<0.
By differentiating the government budget constraint, we derive the relation between tax rate variations implied by the condition of revenue-neutrality[10]
. We obtain:
![]()
(7).
The second subscripts (i = 1,n) indicate the price with respect
to which every element of the vector is differentiated. The term ![]()
is the ratio between the marginal revenue of the two taxes affected by the
reform ![]()
.
We assume that both taxes are revenue increasing, so that the ratio between
the two marginal revenues is positive, i.e. ![]()
.
Equation 6 can now be written as:
![]()
(8).
where RRPi, the revenue potentiality, is the ratio between the
marginal revenue of tax i and its base (MRi/xi) and
![]()
is the distributional characteristic of good i (i=1,n). The definition of distributional characteristic is due to Feldstein (1972) and is related to the relationship between social weights and share of consumption by different classes of consumers. Its value is high when a good is mainly consumed by consumers whose welfare is valued more in the social welfare function (the poor). The revenue potentiality measures the ability to raise new revenue by marginally increasing the tax rate.
In equation 8, the change in tn is negative by definition of the
reform and the term ![]() is always positive. Hence, the sign of the welfare effect of the reform
depends only on the term in square brackets.
is always positive. Hence, the sign of the welfare effect of the reform
depends only on the term in square brackets.
Equation 8 has remarkable empirical relevance because none of the elements
requires the specification of a function of utility in
order to represent
consumers’ welfare. The marginal revenue can be estimated through the
analysis of the relationship between
total revenue and the tax rates, exploiting
for example evidence from previous tax reforms or historical data. The value of
consumers
expenditure in commodities is found in national accounts or social
accounting matrices released periodically by national institutes
of statistics.
Nevertheless, the empirical literature on the evaluation of tax reforms has not
exploited this result[11]. The ratio
between the two revenue potentialities, hereafter ![]()
, picks up the efficiency effects of the reform. In fact, if all consumers
are given the same social weight (γA=γB=1) or if
all goods are consumed in the same proportion by poor and rich families, the
ratio between the distributional characteristics
of the two goods (is equal to 1
and) no longer appears in equation 8. In these cases, only efficiency matters
and the welfare effect
of the reform can be studied by looking at the revenue
potentialities only. In particular, tax reforms increase welfare when the
tax
burden is transferred from taxes with low revenue potentiality to taxes with
high revenue potentiality, i.e. when ![]()
. The intuition behind this result is that taxes which can produce revenue “more easily” generate less distortions. On the other hand, the effect of the reform on distribution are picked up by the distributional characteristics of the goods. Equity improves if the reform shifts the tax burden towards goods with lower distributional characteristics. This “distributional benefit” must be compared with efficiency effects in order to determine if the reform is socially desirable. Overall, social welfare increases when the following condition holds:
![]()
(9).
If the reform increases efficiency (α<1) and the tax burden is shifted towards goods consumed mainly by better–off individuals (the ratio between the two distributional characteristics is bigger than one), then social welfare increases. This is the set of reforms which improve both efficiency and distribution. However, it is now possible that social welfare increases also if efficiency decreases (α>1), as far as the ratio between the two revenue potentialities is smaller than the ratio between the distributional characteristics. In these cases, efficiency decreases but distribution improves, and the latter effect is big enough to offset the former.
Condition 9 provides a policy rule for the decision maker. As pointed out above, revenue potentialities can be estimated from data on the relationship between total revenue and tax rates; consumption by different (groups of) consumers is estimated through household surveys. The most problematic issue is in the determination of social weights for consumption by different individuals (or groups). An analysis of sensitivity – as suggested by Ahmad and Stern (1984) – would probably be most appropriate, with the determination of the sets of weights which are consistent with an increase in social welfare. An example is provided later on in the paper.
In some cases, however, it is possible that the structure of the distribution of consumption among different individuals guarantees an increase in social welfare, whichever the value of the weights in the social utility function. The concept of marginal conditional welfare dominance – proposed by Yitzhaki et al. (Yitzhaki and Thirsk (1990) , Slemrod and Yitzhaki (1991), Mayshar and Yitzhaki (1995)) – can be used to select a couple of tax rates whose change, in the context of a revenue-neutral reform, is desirable according to every social welfare function which reflects a non-negative degree of aversion to inequality[12]. A tax dominates another one when it bears on a good whose consumption is relatively lower among poor people and when its revenue potentiality is not lower. For this purpose, it is useful to express equation 6 as follows:
![]()
(10).
Expression 10 corresponds to equation 7 of Yitzhaki and Thirsk (1990, p. 6), but now α is the ratio between the two revenue potentialities. If the concentration curve of commodity n lies above the concentration curve of commodity 1, multiplied by the efficiency parameter α, then:
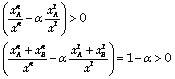
(11),
which can be restated as follows:
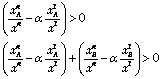
(12).
If γA≥γB, this is a sufficient condition for:
![]()
(13),
which ensures an increase in social welfare.
In this case, t1 dominates tn. The same
result cannot be reached if the reform increases tax distortions
(α>1). In this case, in fact, ![]()
, so that at least in the case in which all social weights are equal to each other (γA=γB), the sign of 10 is negative (Yitzhaki and Thirsk, 1990).
It follows that social welfare increases for every social utility function with a non-negative degree of aversion towards inequality if the reform shifts the burden of taxation towards taxes which levy revenue more easily and if the ratio between the two revenue potentialities is lower than the ratio between the shares of consumption, i.e. if the following conditions hold:
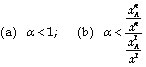
(14).
Condition 14 is evidently more restrictive than 9. In this case, the possibility that a decrease in efficiency is compensated by an improvement in distribution is not allowed. When (almost) no structure is imposed on the social welfare function, it is necessary at least that efficiency does not decrease (first part of 14). However, if efficiency increases, it is not necessary that the tax burden is shifted towards taxes that are consumed mainly by poor individuals. In some measure, the second part of condition 14 allows that the share of consumption by the poor of the good whose tax increases is bigger than the share of consumption by the poor of the good whose tax decreases, as far as the ratio between the two shares is bigger than the ratio between the revenue potentialities.
The above suggestions can be integrated in order to define a procedure that can be followed by the policy maker who wishes to evaluate the efficiency and distributional effects of a revenue-neutral tax reform. The policy maker can hence proceed as follows:
1. estimating the revenue potentiality of the taxes whose rate is affected (and calculate the parameter α): this is sufficient in order to evaluate the efficiency effects of the reform (efficiency improves if α<1);
2. comparing the modified concentration curves of consumption of the two goods: this may identify cases of welfare dominance, in which the reform increases social welfare for any social utility function which reflects a non-negative degree of aversion to inequality – a very general (and safe) conclusion; in our case this boils down to (knowing the poor people’s share of consumption of each good and) verifying that 14 holds;
3. if there is no opportunity of welfare dominance, identifying the social weights which are consistent with an increase in social welfare, given the revenue potentialities. In fact, equation 8 can be worked out in order to find the value of the ratio of γA to γB necessary for the condition to hold. This is given by the following expression.
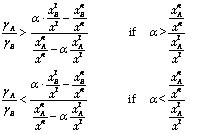
(15)
With this procedure in mind, we can now move to an empirical application of the theory.
The purpose of this section is to provide an example of how the opportunity of consumption tax reforms can be enquired by the policy maker, taking into account both efficiency and equity. We make reference to Italian data for 1993 [13].
The original data allowed distinguishing thirty sectors/commodities, with consumption distributed among six groups of families, ranked according to household income. Here we restrict the analysis to sixteen main commodities, whose final consumption is taxed and exceeds 2.5 billion Euros in value[14] (converted from Italian Lira 1993). This threshold is chosen arbitrarily with the aim to focus on main categories of consumption. Furthermore, in order to keep the analysis simple and consistent with the model outlined above, we aggregate families in two groups, their income being below or above 18,612 Euros (Euros 1993, correspondent to 36 million Italian Lira 1993). This subdivision corresponds to median household income (data from the Household Budget Survey of the Bank of Italy for 1993) and ideally divides Italian families in two groups, the poorer and the richer.
Table 1 reports the composition of consumption in Italy in 1993.
The single most important voice, in terms of value, is processed food (Food products, tobacco and alcoholic beverages), whose purchases amount to 63 billion Euros; together with commodities purchased directly from the primary sector (Agriculture, cattle, forestry and fishing), this constitutes most of Italian household food expenditure (part of the consumption in “Hotels and restaurants” should still be added to complete the picture). Among the other most important components of consumption, in terms of value, we find “Hotels and restaurants”, “Other services” and “Textiles”.
Table 1 provides also evidence about the distribution of consumption between poorer and richer families. The share of consumption by poor households ranges from a minimum of 21 percent for “Chemicals and pharmaceutical” products and “Other services” to a maximum of 42 percent for processed and unprocessed food items.
Table 1, eventually, reports the revenue potentiality of each single consumption tax, estimated through simulations of marginal tax rate changes in a numerical model of the Italian economy[15]. Additional revenue can be obtained with the lowest cost in terms of efficiency (we could say most easily) by increasing the tax rate on the consumption of unprocessed food items (RRP=0.009237) and electrical equipment (RRP=0.009215). At the other extreme, the taxation of energy consumption is most distortionary and new revenue can be risen from it only at high efficiency costs (RRP=0.007192) – though this statement considers consumption distortions only and does not account for environmental externalities.
A policy maker interested in modifying a couple of tax rates within a revenue neutral tax reform and who cares for both efficiency and equity can start by verifying if conditions 14 hold. In this case, social welfare would increase for every social utility function consistent with a non-negative degree of aversion to inequality. It would not be necessary to quantify the preference for poor people’s welfare with respect to rich people’s, i.e. to set γA and γB, but only to accept that the former is not less important than the latter, i.e. that γA≥γB. Table 2 shows the results of all possible tax reform. Rows refer to the goods whose tax rate increase, columns to the ones whose tax decrease. Cells background is shaded when the first of the two conditions holds, i.e. when the reform increases efficiency (the revenue potentiality of the tax which grows is higher than the revenue potentiality of the one which decreases, hence α<1). In a subset of cases, the reform is desirable on both efficiency and distributional ground, when both conditions 14 hold. We mark the corresponding cells with a 1. These are the reforms that the policy maker can realize more safely, with no need to make social weights explicit. Cells containing a 0 represent the cases in which we cannot be sure that social welfare increases, independently from the efficiency effect of the reform. In order to make a decision, it is necessary to know more about the structure of the social welfare function.
Though Table 2 provides evidence about the effects of all possible reforms, we will comment only on a few cases. In particular, we will focus first on reforms that increase the taxation on electrical equipment, the set of commodities with the second highest revenue potentiality. In addition to low distortionary power, electrical equipment have very favorable distributional characteristics, with only 21 percent of consumption ascribable to poor families. We will also consider the possibility to increase the taxation on the consumption of chemical and pharmaceutical products, as the distributional characteristics are once more favorable and because chemical industries are likely to be responsible for negative environmental externalities (concerns for the health of the poor are ruled out by the fact that drugs are actually paid by the public sector through the national health service). We abstain from considering the possibility to decrease the tax on energy products, which is characterized by the lowest revenue potentiality, because energy consumption is associated with the production of major negative environmental externalities. It is possible that the high level of taxation on this category of commodities is due to the will to correct such distortions and set the right incentives for private choices (at least in part it should be this way). Our model could accommodate externalities and be used to derive a decision rule for cases in which consumption distortions and other distortions change in opposite directions, creating a trade-off, but this goes beyond the scope of the present paper. Among the sectors whose taxation may be reduced in order to ensure revenue neutrality, we will consider processed food and textiles. Cases on which we comment are bordered in the tables.
Increasing taxes on electrical equipment (sector 9) and reducing taxation on processed food (sector 11, as well as on textiles (12)) in order to guarantee revenue neutrality actually satisfies both conditions 14 and constitutes a welfare improving reform[16]. The same is true for the reform which increases taxation on chemical items (sector 5) and decreases the rate on textiles, but not for the one in which revenue neutrality is ensured by lower taxes on processed food. In this case, the efficiency condition does not hold: despite the fact that processed food is characterized by a much higher share of consumption allocated to the poor, the fact that the tax on chemicals has a lower revenue potentiality implies that welfare would decrease if both groups of households were given the same weight in the social welfare function. This is a case in which the policy maker can justify the reform only by making social weights explicit.
This allows introducing the following step of the analytical process. In cases in which conditions 14 do not hold, the policy maker is forced to make the set of social weights explicit. In Table 3, in order to provide a simple example, reforms are evaluated on the basis of a social welfare function in which poor people’s welfare is valued twice as much as rich people’s (γA=2γB).
The value “1” marks the cases in which social welfare is found to increase. The background of the cell is shaded in the cases in which conditions 14 hold (which is of course a subset of the cases in which welfare increases), i.e. those in which social welfare increases according to any social utility function with a non-negative degree of aversion to inequality.
Assigning a higher weight to poor people’s welfare remarkably increases the relevance of distributional consideration with respect to efficiency. Table 3 shows that reducing the tax on unprocessed food (sector 11) is now convenient in most cases, despite the high value of its revenue potentiality, thanks to the high share of these goods consumed by poor households and to the high value assigned by the policy maker to the welfare of this category.
When poor people’s welfare is assigned double value, also the reform which increases the tax on chemical products and reduces the tax on processed food turns to be socially desirable. However, giving double value to poor people’s welfare is not necessary in order to obtain this result. For any cell in Table 3, the policy maker can determine the minimum value of γA necessary in order to make the reform convenient, according to equation 15. In this specific case, any value above 1.053 guarantees that condition 8 holds – indeed a very reasonable degree of preference for poor.
This paper deals with revenue-neutral marginal commodity tax reforms in economies with heterogeneous individuals. In a simple model with two classes of consumers, we originally develop a decision rule based on revenue potentialities. The relationship with the streams of research dealing with specific weights in the social welfare function (Ahmad and Stern (1984)) and looking for cases of welfare dominance ((Yitzhaki and Thirsk (1990); Mayshar and Yitzhaki (1991)) is analyzed.
The use of a simple two consumers model makes the relationship between efficiency and distributional considerations particularly explicit. The former can be studied in terms of ability of different taxes to collect new revenue, an indicator of distortion which does not depend on assumptions about utility functions. The latter is related to shares of expenditure by poor and rich for the different goods involved in the reform.
The analysis allows defining a procedure that the policy maker can follow in order to identify welfare increasing opportunities, starting from the lowest amount of hypothesis, structure and information. When the most desirable opportunities are not available, the policy maker can identify welfare improving commodity tax reforms only by imposing more structure. Operationally, the first step is to study the effects of the reform in terms of efficiency, i.e. to measure the revenue potentiality of different taxes. These indicators can be used together with information on distribution of consumption in order to determine if the reform in which the policy maker is interested increases welfare according to any social welfare function characterized by a non-negative degree of aversion towards inequality. If this does not happen, the policy maker can calculate the minimum degree of preference for the worse-off group (with respect to the better-off) necessary to make the reform socially desirable – and check if this assumes a sensible value, upon which society can agree.
- Structure of final consumption (Italy, 1993)
|
Sector
|
|
RRP
|
Consumption (billion Euros) by families with income
|
Total (billion Euros)
|
Share consumed by most poor
|
|
|
below 18.612 Euro
|
above 18.612 Euro
|
|||||
|
Agriculture, cattle, forestry, fishing
|
1
|
0.009237
|
11.766
|
16.277
|
28.043
|
0.420
|
|
Energy products
|
2
|
0.007192
|
8.988
|
15.409
|
24.397
|
0.368
|
|
Chemicals and pharmaceuticals
|
5
|
0.008299
|
4.691
|
16.797
|
21.488
|
0.218
|
|
Electrical equipment
|
9
|
0.009215
|
2.081
|
7.678
|
9.760
|
0.213
|
|
Transport equipment
|
10
|
0.008421
|
4.038
|
14.380
|
18.418
|
0.219
|
|
Food products, tobacco, alcoholic bev.
|
11
|
0.008387
|
26.443
|
36.580
|
63.023
|
0.420
|
|
Textiles, made-up textile articles
|
12
|
0.008244
|
9.756
|
27.538
|
37.294
|
0.262
|
|
Leather, footwear
|
13
|
0.008258
|
3.078
|
8.689
|
11.767
|
0.262
|
|
Wood, wood furniture
|
14
|
0.008331
|
2.675
|
8.345
|
11.021
|
0.243
|
|
Paper, printing, publishing
|
15
|
0.008117
|
1.877
|
6.924
|
8.801
|
0.213
|
|
Miscellaneous manufacturing
|
17
|
0.008109
|
2.485
|
8.727
|
11.213
|
0.222
|
|
Recycling, repair
|
19
|
0.008327
|
2.312
|
8.232
|
10.544
|
0.219
|
|
Hotels and restaurants
|
21
|
0.008785
|
8.880
|
31.183
|
40.063
|
0.222
|
|
Land transport, transport via pipelines
|
22
|
0.008648
|
1.215
|
4.325
|
5.539
|
0.219
|
|
Communications
|
25
|
0.008472
|
1.045
|
3.720
|
4.765
|
0.219
|
|
Other service activities
|
29
|
0.008454
|
9.013
|
32.269
|
41.282
|
0.218
|
- Tax reforms which increase welfare according to any SWF with a non-negative degree of aversion to inequality. Shaded background indicates cases in which efficiency would increase. Value 1 indicates that SW would increase according to any SWF with a non-negative degree of aversion to inequality (a subset of shaded cells).
|
|
Sector whose tax rate descreases (n)
|
||||||||||||||||
|
1
|
2
|
5
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
17
|
19
|
21
|
22
|
25
|
29
|
||
|
Sector whose tax rate increases (1)
|
1
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
2
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
|
5
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
|
|
9
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
|
10
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
|
|
11
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
|
12
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
|
13
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
|
14
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
|
15
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
|
|
17
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
|
19
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
|
|
21
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
|
|
22
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
|
|
25
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
|
|
29
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
|
– Tax reforms which increase social welfare for specific weights. Specific case γA=2γB. Value 1 indicates that SW increases. Shaded background indicates that SW would increase according to any SWF with a non-negative degree of aversion to inequality.
|
|
Sector whose tax rate descreases (n)
|
||||||||||||||||
|
1
|
2
|
5
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
17
|
19
|
21
|
22
|
25
|
29
|
||
|
Sector whose tax rate increases (1)
|
1
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
2
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
|
5
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
|
|
9
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
|
10
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
|
|
11
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
|
12
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
|
13
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
|
14
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
|
|
15
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
|
|
17
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
|
19
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
|
|
21
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
|
|
22
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
|
|
25
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
|
|
29
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
|
The extension of the model presented above to an economy with H consumers (H>2) is straightforward, as most relationships are additive.
The social welfare function can be expressed as follows:
![]()
(A.1).
The relationship between the change in the two tax rates affected by the reform, such to keep revenue constant, is given by the following expression.
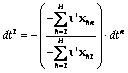
(A.2)
The ratio between the two revenue potentialities is given by:
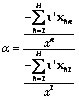
(A.3),
and the formula for the change in social welfare caused by the reform does not change, though now the distributional characteristic is defined as:
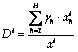
(A.4).
Once again, the reform increases social utility if the following condition holds:
![]()
(A.5).
The interpretation in terms of relationship between (the ratios of) revenue potentialities and distributional characteristics does not change.
Expression 10 can now be expressed as follows:
![]()
(A.6).
If the concentration curve of good n lies below the concentration curve of
good 1, multiplied by the ratio between the two revenue
potentialities, then
![]()
is a succession of positive terms. If individuals are ranked so that the social weights (γh) are non-increasing in h, this is a sufficient condition for the following expression to hold:
![]()
(A.7),
hence for social welfare to increase.
In this case, the condition for an improvement in welfare cannot be reduced to a comparison between revenue potentialities and consumption shares. Social welfare increases according to any social utility function characterized by a non-negative degree of aversion to inequality if efficiency does not decrease and the concentration curve of the good whose tax decreases lies above the concentration curve of the good whose tax increases, the latter multiplied by the ratio between the revenue potentialities.
Accardo, B.M., B. Cavalletti and A. Pench, (2002), “Il Modello IT30: Dati e Struttura”, in F. Bulckaen, A. Pench and M. Stampini (eds), Riforme Fiscali e Politiche Ambientali, Franco Angeli, Milano, pp. 61-111.
Ahmad, E. and N. Stern (1984), “The Theory of Tax Reforms and Indian Indirect Taxes”, Journal of Public Economics, 25: 259-98.
Atkinson, A.B. and J.E. Stiglitz (1976), “The Design of Tax Structure: Direct Versus Indirect Taxation”, Journal of Public Economics, 6: 55-75.
Auerbach, A.J. and J.R. Hines Jr. (2002), “Taxation and Economic Efficiency”, in A.J. Auerbach and M. Feldstein (eds), Handbook of Public Economics, Ch. 21, Vol.3, Elsevier Science B.V..
Bulckaen, F. (1992), “The Theory of Commodity Tax Reform: A Survey”, in G. Galeotti and M. Marrelli (eds), Design and Reform of Taxation Policy, Kluwer Academic Publishers, Dordrecht.
Bulckaen, F. and M. Stampini (2001), “Efficiency and Distributional Effects of Revenue-Neutral Green Tax Reforms”, Studi Economici, 1: 25-38.
Bulckaen, F., A. Pench and M. Stampini (2003), “Evaluating Tax Reforms Without Utility Measures: The Performance Of Revenue Potentialities”, Discussion Paper n.7, Department of Economic Science at the University of Pisa.
Corlett, W.J. and D.C. Hague (1953-54), “Complementarity and the Excess Burden of Taxation”, Review of Economic Studies, 21: 21-30.
Deaton, A.S. (1987), “Econometric Issues for Tax Design in Developing Countries”, in D.M.G. Newbery and N.H. Stern (eds), The Theory of Taxation for Developing Countries, Oxford University Press, New York.
Dixit, A.K. (1975), “Welfare Effects of Tax and Price Changes”, Journal of Public Economics, 4: 103-123.
Feldstein, M. (1972), “Distributional Equity and the Optimal Structure of Public Prices”, American Economic Review, 62(1/2): 32-36.
Gordon, J.P.F. (1989), “A Many Good, Many Person Corlett-Hague Rule”, Economic Letters, 29: 157-161.
Guesnerie, R. (1977), “On the Direction of Tax Reform”, Journal of Public Economics, 7: 179-202.
Hatta, T. (1986), “Welfare Effects of Changing Commodity Tax Rates Toward Uniformity”, Journal of Public Economics, 29: 99-112.
Kaplow, L. (2004), “On the Undesirability of Commodity Taxation Even when Income Taxation is not Optimal”, NBER Working Paper n. 10407.
Mayshar, J. and S. Yitzhaki (1995), “Dalton-Improving Indirect Tax Reform”, American Economic Review 85(4): 793-807.
Slemrod, J. and S. Yitzhaki (1991), “Welfare Dominance: an Application to Commodity Taxation”, American Economic Review 81(3): 480-96.
Slemrod, J. and S. Yitzhaki (1996), “The Social Cost of Taxation and the Marginal Cost of Funds”, International Monetary Fund Staff Papers, 43, 1, (March).
Yitzhaki, S. (2003), “Cost-Benefit Analysis and The Distributional Consequences of Government Projects”, National Tax Journal, Vol. LVI, No. 2 (June): 319-336.
Yitzhaki, S. and W. Thirsk (1990), “Welfare Dominance and the Design of Excise Taxation in the Côte D’Ivoire”, Journal of Development Economics, 33: 1-18.
[♣] Sant’Anna School of Advanced Studies, Piazza Martiri della Libertà 33, 56127, Pisa, Italy. Corresponding author: Marco Stampini, e-mail: stampini@sssup.it. We would like to thank the participants in the seminar held at the Department of Economics of the University of Pisa (June 2004) and one anonymous referee for useful comments. Remaining errors are our own.
[1] Though we always refer to marginal tax reforms, the adjective “marginal” is often omitted along the paper.
[2] For an updated overview of the literature on optimal taxation, see Auerbach and Hines (2002). For a survey on commodity tax reform, see Bulckaen (1992).
[3] The concept of distributional characteristic was introduced by Martin Feldstein (1972), who dealt with optimal pricing by a public enterprise producing several goods in a multiple consumer economy. His conclusions imply that, when social preferences depend negatively on inequality, tax reforms which increase the rates on goods mainly consumed by better-off people and decrease tax rates on goods mainly consumed by worse-off people are more likely to increase social welfare.
[4] Alternatively, the policy maker can try identifying those weights that are implicitly consistent with the current – observed – situation, i.e. those weights which make the observed tax rate structure optimal. If those weights are obviously unacceptable, it means that there exist opportunities for welfare improving tax reforms. In particular, if some of these weights are negative, then a pareto-improving tax reform is possible.
[5] A similar problem of complexity (of the underlying hypothesis) affects the conclusions of Deaton (1987), who tries to identify the conditions that justify a reform towards uniform taxation starting from differentiated tax rates.
[6] The concentration curve
“measures the fraction of total expenditure on a commodity that can be
ascribed” to the first
j percent of the population, once
individuals have been ranked – i.e. ordered on the base of an index of
need chosen by the policy-maker
(Yitzhaki and Thirsk, 1990, p. 2). The
concentration curve of the arbitrary commodity i (i=1,...n) is
given by the function ![]() , where
, where ![]() represents consumption of commodity i by household
h,
represents consumption of commodity i by household
h, ![]() is
total consumption of i, and individuals are ranked. A possible example of
ranking index is the level of expenditure in non-durable commodities.
is
total consumption of i, and individuals are ranked. A possible example of
ranking index is the level of expenditure in non-durable commodities.
[7] The theoretical model shows that the distribution of welfare, the object of our interest, can be studied through the analysis of the distribution of expenditure on commodities.
[8] In what follows, the apex refers to the good (xi, i=1,…n), boldface type indicates a vector (x) and prime indicates vector transpose (´). The first subscript indicates the individual (h=A, B), the second subscript (i=1, n) indicates the derivative, the gradient or the Jacobian matrix of the element with respect to price i (xAi, xBi).
[9] A labor tax which reduces wage proportionally is equivalent to a flat commodity tax on all commodities.
[10] The budget constraint of the public sector is given by:
![]()
Hence:
![]()
is the marginal revenue of tax i. By differentiating the budget constraint of each individual consumer we obtain:
![]()
![]() .
.
It follows that the marginal revenue (MR) of tax i can be expressed as follows:
![]() .
.
[11] This may be due to the fact that expression 8 is exactly valid in the simple theoretical model used by the literature on tax reforms. Applied works try to replicate more complex economies, characterized for example by the presence of intermediate goods, international trade and multiple forms of taxation. The validity of the simple rule in complex systems needs empirical testing. A recent work by Bulckaen et al. (2003) deals with the problem and finds encouraging results, supporting the use of revenue potentialities for the evaluation of the efficiency effects of commodity tax reforms, hence also the use of expression 8 in a many-consumers setting.
[12] The analysis can be extended to reforms which involve more tax rate changes, following Mayshar and Yitzhaki (1995).
[13] For details, see Accardo et al. (2002). The last social accounting matrix released by the Italian institute of statistics (ISTAT) dates back to 1992. More recent consumption data is made available by the Survey on Consumption by Italian Households; nevertheless, we use data from 1993 (obtained by updating the 1992 SAM), because the availability of a SAM allows estimating the revenue potentiality of different consumption taxes through a general equilibrium simulation. The explanatory value of the analysis is not diminished by this choice, though of course the relevance in terms of current policy recommendations does.
[14] An exception is made for the sector “Communication”, whose consumption value is slightly lower than the threshold.
[15] A Computable General Equilibrium model of the Italian economy - with quite standard characteristics but a very detailed modelization of the tax system - is used. Revenue potentialities are calculated by simulating the effect on total revenue of a one percent increase in each tax rate. Details can be found in Bulckaen et al. (2003).
[16] In the present analysis, we are assuming perfect information. In the real world, the policy maker will be interested in evaluating the degree of confidence of the indications of each policy rule. This could be done, for example, by performing a sensitivity analysis of the main assumptions of the model used to calculate the revenue potentialities. In other cases, if the parameters are estimated econometrically, they will be associated with an interval of confidence. In this exemplification, we keep things as simple as possible.
AustLII:
Copyright Policy
|
Disclaimers
|
Privacy Policy
|
Feedback
URL: http://www.austlii.edu.au/au/journals/eJlTaxR/2005/8.html